*追記 より処理を効率化した変換処理の説明記事はこちら。
自作のtoComp関数です。標準のtoComp()が使えない場合などほぼないですが、座標変換の理解としてお役立て下さい。
function mToComp(aLyr, aTgtPt) {
var mTfms = [];
var mPrtLyr = aLyr;
var mCntr = 1;
var mHasPrtOrNot = true;
//階層をさかのぼって先祖のないレイヤーになるまで処理を続ける(上限は100回にしてある)。
while ( mHasPrtOrNot === true ) {
if( mPrtLyr.hasParent === false){
mTfms.push(mPrtLyr.transform);
mHasPrtOrNot = false;
break;
}else{
mTfms.push(mPrtLyr.transform);
mPrtLyr = mPrtLyr.parent;
mCntr++;
}
}
//先祖から順に処理するので、反転する。
mTfms.reverse();
//-------------------------------------------------------------------------
//非歪位置(各トランスフォームのApのコンポ座標)を親から順に割り出して、mEachPts配列に入れていく。
var mEachPts = [];
for (var i = 0; i < mTfms.length; i++) {
if (i === 0) {
var mXY = mTfms[0].position;
mEachPts.push(mXY);
} else {
//子の位置は親の“原点からの”位置なので、前回算出位置から現状の親のアンカーポイントを引いて、現状ループの位置を足す。
mXY = mXY - mTfms[i - 1].anchorPoint + mTfms[i].position;
mEachPts.push(mXY);
}
}
//TgtPtの非歪コンポ座標を出す。
//ループ後のXYはラストレイヤーのアンカーポイント位置になるので、アンカーポイントを引いて原点にし、そこにTgtPtを足す。
var mTgtXY = (mXY - mTfms[mTfms.length - 1].anchorPoint) + aTgtPt;
//-------------------------------------------------------------------------
//スケール、回転を子から順に設定していく。まずは子~親順にする。
mTfms.reverse();
mEachPts.reverse();
//自身が所属するトランスフォームも含めて処理するので、length分全てを回す。
for (var i = 0; i < mTfms.length; i++) {
//スケールパート。計算しやすいように原点からの位置にして、スケーリングして元の位置に戻す。
var mVecXY = mTgtXY - mEachPts[i];
var mScldX = mVecXY[0] * (mTfms[i].scale[0] / 100);
var mScldY = mVecXY[1] * (mTfms[i].scale[1] / 100);
mTgtXY = [mEachPts[i][0] + mScldX, mEachPts[i][1] + mScldY];
//回転パート。
//親が設定している角度から、結果の位置を割り出す(親とTgtPt間の現状の角度は関数内で考慮されている)。
mTgtXY = mGetRotPt(mEachPts[i], mTgtXY, mTfms[i].rotation);
}
return mTgtXY;
//以下、関数内で使用している関数。
//------------------------------------
//2点から、基準点を中心に目標点を回転させた値を得る(現状の2点の角度は入れなくてよい)。
function mGetRotPt(aStdPt, aTgtPt, aStdRot ) {
var mTgtPtZr = aTgtPt - aStdPt;
var mRotRd = aStdRot * (Math.PI / 180);
var mRstX = mTgtPtZr[0] * Math.cos(mRotRd) - mTgtPtZr[1] * Math.sin(mRotRd);
var mRstY = mTgtPtZr[0] * Math.sin(mRotRd) + mTgtPtZr[1] * Math.cos(mRotRd);
return [mRstX,mRstY]+aStdPt;
}
}通常のtoComp()は○○.toComp(座標)ですが、これはmToComp(○○,座標)と入力してお使いください。
使いどころ
エクスプレッションに関してはとくにないんですよね…。しかし、シェイプレイヤーの中にあるシェイプグループのトランスフォームは標準の変換メソッドが使えないので、その関数を作る知識への橋渡し的なものとして参照ください。
これ自体はシェイプレイヤーのトランスフォームに対応しておりません。
ただ、AEスクリプトには変換メソッドが無いので、前半の『さかのぼって先祖レイヤーを得ていく』作業だけ、スクリプト用に書き換えれば使えます。しかし、これも「スクリプトでいったん仮のポイント制御を作り、そこにtoCompエクスプレッションを適用して値を得て、仮ポイント制御を消す」という実装にしたほうが、確実です。自作のものを使う利点としては、「仮ポイント制御を消す作業をしたことで、選択プロパティの変数へのリンクが全部外れる」ことがない、ということですね。
解説
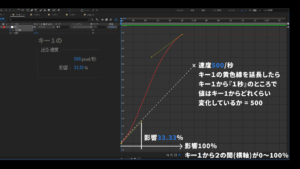
要するにやりたいのは「今、パラメータから得られる情報だけで、AEが座標計算した経緯を追計算する。ただし目標点だけはグローバル座標であることを保持しながらやる」ってことですね。
なかなか解説が難しいので、映像にしてみました。
fromCompも同じ要領で、逆に回転スケールを元に戻していくことで得ることができます。
各点のグローバル座標を得るまでは一緒です。その各点を軸に目標グローバル点を逆回転、逆スケールして、位置移動していきます。すると、目標グローバル点は『各レイヤー回転スケールなし状態』に対応した位置になります。この状態だと、レイヤー座標とコンポ座標のマス目単位が一緒なので、『得たいレイヤー座標のレイヤー原点』から見た、移動させた目標グローバル点がレイヤー座標での位置となります。なので「移動させた目標グローバル点 ー 得たいレイヤー座標のレイヤー原点」でレイヤー座標が得られる、という具合です。
注意点としては、toCompの逆で、回転、スケールの順で行うということと、親から順に計算するということですね。もしも興味があれば上記エクスプレッションを書き換えてみてください。
座標変換といえば「『線形代数』『アフィン変換』『行列』を理解すれば効率的な変換が可能になるらしい」という情報を得たのですが、今だ未確認です。書籍だけ、買った状態ですね!