【エクスプレッション】パスの長さを得る

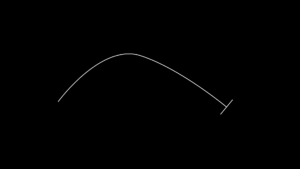
誤差が1ピクセル位ありますが、エクスプレッションでパスの全長をかんたん、高速に得ることができます。
追記　条件によっては実用できないほどの誤差が出るので、修正を加えました。詳細は後述です。

■新バージョン（誤差を修正しました）

function mGetPathLengthOverAll( aPath ){ 
	var mPowLgt = 0;
	var mTgtPts = [];
	for( var i = 0; i < 10; i++ ){
		var mRatio1 = 0.01 * i;
		var mRatio2 = 0.01 * (i+1);
		var mPt1 = aPath.pointOnPath(mRatio1);
		var mPt2 = aPath.pointOnPath(mRatio2);
		var mPowLgtDiv = Math.pow(mPt2[0] - mPt1[0], 2) + Math.pow(mPt2[1] - mPt1[1], 2);
		if( mPowLgt < mPowLgtDiv ){
			mTgtPts = [mPt1,mPt2];
			mPowLgt = mPowLgtDiv;
		}
	}
	var mLgt = length( mTgtPts[0],mTgtPts[1] );
	return mLgt * 100;
}

■旧バージョン（誤差がけっこう出る場合があります）

function mGetPathLengthOverAll( aPath ){ 
	var mPt1 = aPath.pointOnPath(0);
	var mPt2 = aPath.pointOnPath(0.01);
	var mLgt = length( mPt1,mPt2 );
	return mLgt * 100;
}

使い方

//この上にmGetPathLengthOverAllがコピペしてある。

var mPath = thisComp.layer("シェイプレイヤー 1").content("シェイプ 1").content("パス 1").path;
var mLgt = mGetPathLengthOverAll(mPath);
mLgt/101;

使いどころ

例にもある通り、破線の計算に使えます。「最後だけちょっと実線が短い破線」ができたときにいちいち調整しなくてよくなります。他にも何かに使えそうです。

解説

パスのメソッドpointOnPath()は ( ) の中に0～1を入れると、始点をゼロ、終点を１とした中間点の位置を得てくれます。
わかりやすく言えば、0％～100％の代わりに0～１を入れればよいということですね。パスのちょうど半分の位置を知りたいときは『パス.pointOnPath(0.5)』という具合です。
そして、％に置き換えられることからもわかるように、0～１は等間隔です。
なので、パスの始点位置とそこからちょっとだけ（0.01）進んだ位置の距離を得て、
その距離を残る全長分、足しまくってしまえば全長が出る、ということです。
（足しまくると書きましたが、0.01つまり1％の距離が出たので、×100で100％の距離が出るという計算です）

実際は、1％に細かく分割したとはいえ、直線距離を足しまくっているので、曲線であるパスとは誤差が生まれます。
しかし誤差１ピクセルならば使えるだろう、ということです。
ちなみに、「もっと細かく分割して、その分かける数のケタを増やせば、もっと正確になるだろう」と思うものですが、どうも細かすぎても誤差が出るようで、0.01と×100の組み合わせが一番誤差がないようです。
（おそらくpointOnPath()自体にも実際の位置と誤差があるんだろうなあと思います。予想ですけども）

パスというかベジェ曲線の仕組みは
s.h’s page様の『ベジエ曲線について』という記事が非常にわかりやすくてオススメです。
しかし、ベジェ曲線について知っている人ほどpointOnPath()には注意してください。
始点終点とインアウトハンドルの４点からなるベジェ曲線は、0～1の『T』という値でその中間点を得ることができます。
が、これとpointOnPath()の0～1は『別物』だということに注意が必要です。

ベジェ曲線

• 始点終点とインアウトハンドルの４点でできている曲線。パスの一部。
• Tで得られる中間点は等間隔ではない。

パス

• ベジェ曲線が１つ以上組み合わさってできた曲線。
• pointOnPath()で得られる中間点は等間隔。

つまりpointOnPath()は、パスの中にベジェ曲線が何個あろうとおかまいなしに１つの曲線とみなして、等間隔に0％～100％の位置を得るメソッドということです。

ベジェ曲線を学ぶほど「なんでこんなことができるんだろうなあ」と思うのですが、画面上に実際に描画したときの情報でも保持してるんでしょうかねえ…。
pointOnPath()の他、points()も、スクリプトで得たpath.value.verticesとは微妙に値が異なります。やはりエクスプレッションのほうは描画したときの情報を使っているのかもですね（多分）。

追記

詳しく検証したところ、条件によっては誤差が１ピクセルどころではない場合があったので、エクスプレッション内容を修正しました。
誤差がかなり出る条件とは「パスの始点付近があんまりまっすぐじゃない場合」です。

原因は、始点と、始点にごく近い点の直線距離を目盛りとして採用しているため、その直線と２点間の実際の曲線との誤差があまりに大きいと、誤差も含めて足しまくってしまうからです。

なので、解決方法として、直線距離を出すためにサンプリングする２点を『始点＆そこから0.01の点』以外からも選んでみて、その中で一番曲がっていない２点を選ぶ、という処理を加えました。

具体的には、『始点＆そこから0.01の点』『0.01の点＆0.02の点』…といった具合に0.01ずつずらした２点を10個比較しています。

どの２点間曲線が一番曲がっていないかを選ぶ方法は以下になります。
それぞれの線の、実際の曲線の長さは同じはずです。次に、同じ長さのハリガネ数本を思い浮かべて下さい。
曲がったハリガネは、端と端の直線距離がまっすぐなものよりも短いことがわかります。逆に言えば、直線距離が長ければ長いものほどまっすぐということです。なので、直線距離を比較して１番長いものを選ぶ、ということですね！

ちなみに、距離を出すのはエクスプレッションではlength(位置1,位置2)で出ますが、公式としては
Math.sqrt( Math.pow(位置2[0] – 位置1[0], 2) + Math.pow(位置2[1] -位置1[1], 2) )
となります。
このMath.sqrt()、つまりルートを出すという処理がけっこう重いらしく、『長さを比較するだけならば』ルートを出す前の『２乗になっちゃってる距離』を比較しても問題ないみたいなので、そのようにして処理を軽くしています。
最初の10線比較は２乗距離を使って、どれを使うかわかったらその線だけ改めて距離を出して使う、というイメージです。

「10線全部がかなり曲がってたら結局誤差が出て使えないじゃないの」と思って検証したところ、始点から１割の場所でかなりグニャグニャ曲げない限り、使えないほどの誤差が出ることはなく、実際の使用上は問題ないかと思います！