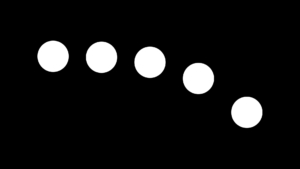
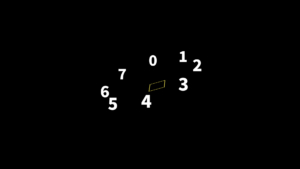
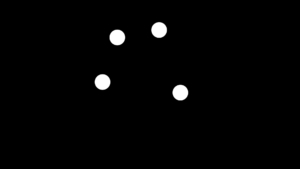
インデックスを使ったエクスプレッションは『レイヤーをコピーするだけで整列』など色々と使えるので、よく使う式を羅列していきます。
欠点の解消
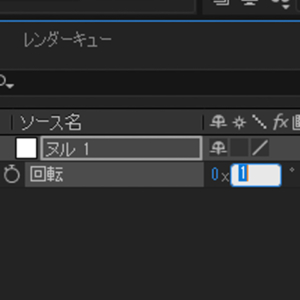
インデックス系エクスプレッションには1つ欠点があります。『インデックスを参照しているがために、上に他レイヤーを置くとインデックスがずれるので置けない』ことですね。これを解消する方法です。
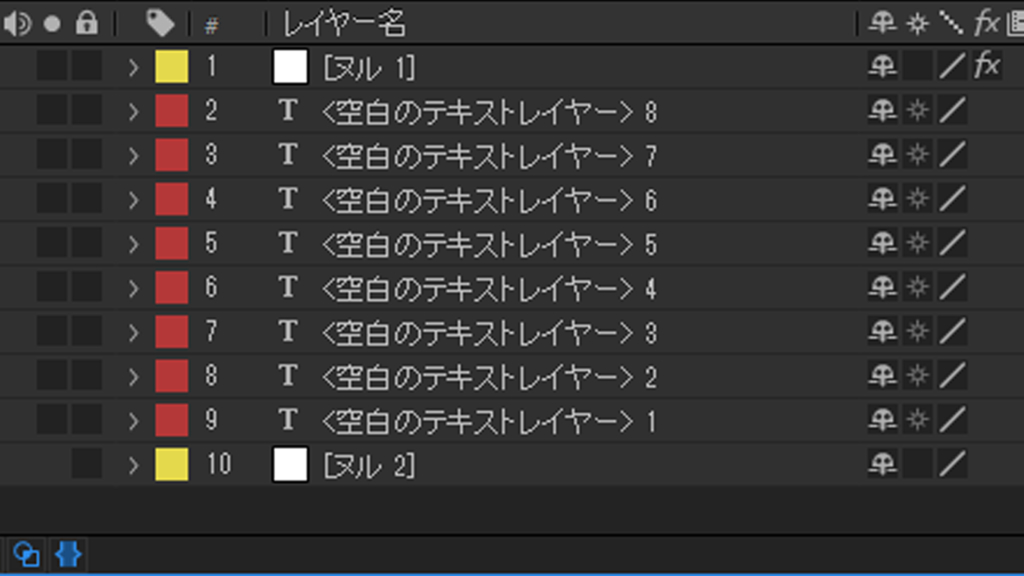
上図のように、エクスプレッションをかける予定のレイヤーをヌル2つで挟んでください。ラベルの色を変えるとよりわかりやすいです。この状態であれば、以下の式でレイヤーの実質インデックスとレイヤー総数が得られます。
mCtrlF = thisComp.layer("ヌル 1");
mCtrlL = thisComp.layer("ヌル 2");
//実質インデックス。
mActIdx = index - mCtrlF.index;
//挟まれたレイヤーの総数。
mActNumLyrs = ( mCtrlL.index - mCtrlF.index ) -1;
これで、ヌル 1の上、ヌル 2の下には好きなレイヤーを置くことが可能となります。
『総数』は使わないときもありますが、たいして重い処理ではないので入れておいてよいかと思います。また総数がいらないときは下のヌルもいらないのですが、「ここからここまでは別レイヤーを入れてはいけません」という目印になるので、あってもよいでしょう。
XY配置で使うインデックス変更式 etc
*これ以降の式は、『欠点の解消』式をまず最初に張り付けてある前提です。
*単純なインデックスエクスプレッションに書き換えたい場合は式中の『mActIdx』を『index』に、『mActNumLyrs』を『thisComp.numLayers』にすればOKです。
■roopEach
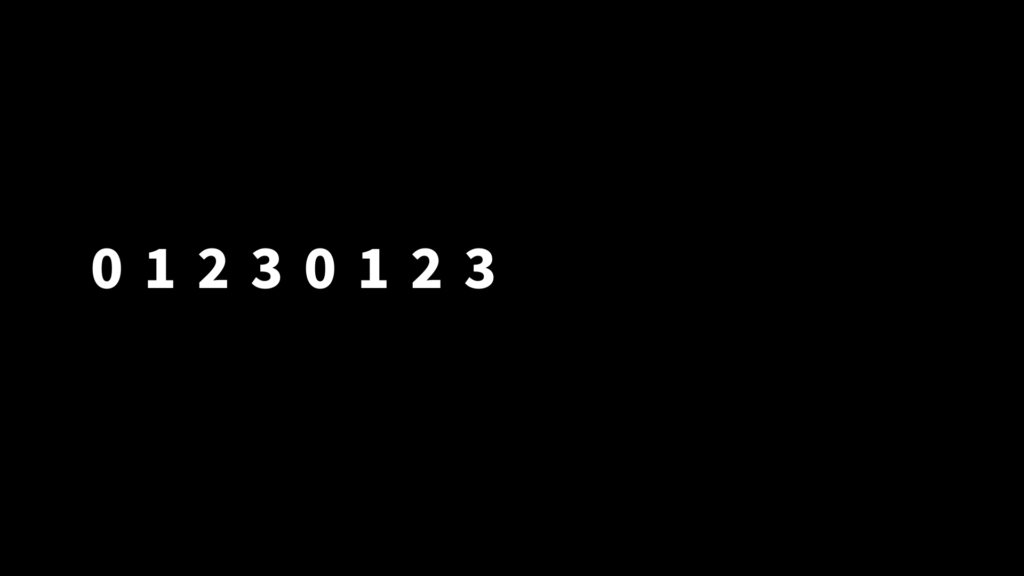
インデックスを特定の番号でループ。
解説:特定の数で割った余りを出せば、ループになります。割り算や余りを使う場合、ゼロ始まりにしないときれいなループにならないため、インデックスからマイナス1しています。
(mActIdx - 1) % 特定の数;■roopMass

インデックスを特定のまとまり数でループ。
解説:インデックス(ゼロ始まりにするためにマイナス1している)を特定の数で割ります。すると、その数に達するまでは小数点付きになるので、小数点を切り捨ててしまえば、達するまで同じ数となります。達したら割り切れるので1増え、またその繰り返し、ということです。
Math.floor( (mActIdx - 1) / 特定のまとまり数 );*上記2つはたいてい、どちらかをX位置、どちらかをY位置に使ってXY整列を実現するために使います。増えていく数を1ずつではなくもっと増やしたい場合は、処理結果に増やしたい倍率を掛ければよいだけです。
■revMinus

インデックスを降順にする。
解説:総数からインデックスを引けば降順になります。
mRevIdx = mActNumLyrs - mActIdx;「インデックス系エクスプレッション部分もいつもと同じくレイヤー積み上げでコンポを組みたいな」といったときに使えます。
■revPlusMinus

インデックスを『ヌル 1』を境に昇順降順入れ替えする。
解説:これは『欠点の解消』式を使いません。ヌルのインデックスからレイヤーのインデックスを引くと、ヌルの上にあるものはヌルから1,2,3…となり、下にあるものはヌルから-1,-2,-3…となります。その結果を絶対値(マイナスもプラスもプラスとする値)にすると、ヌルを境に昇順と降順が入れ替わるインデックスになります。
mCtrl = thisComp.layer("ヌル 1");
mStdIdx = mCtrl.index;
Math.abs( mStdIdx - index );…何かで一度、使った覚えがあります。なんだったっけな…何かに使えます。
■roopReturn

インデックスを特定の番号まで来たら折り返す。
解説:roopEachとRevMinusを組み合わせています。折り返し地点で同じ番号が続くのがなんとなくスッキリしないですが、こちらのほうが蛇のようなうねった並びなどの用途に使えます。スッキリさせるには最後の行の+1を消せばOKです。
//リターンするタイミングの数値。
mDivNum = 特定の数値。
//ゼロ始まりの、このレイヤーのインデックス。
mActIdxZr = mActIdx - 1;
//mDivNum周期で1ずつふえる、ゼロ始まりのカウンター。
mIdxCntr = Math.floor( mActIdxZr / mDivNum );
//カウンターが偶数の場合。
if( mIdxCntr % 2 === 0 ){
//通常の、mDivNumまでいくとゼロに戻る数。
mActIdxZr % mDivNum;
//奇数の場合。
}else{
//行の総数から、通常の増えていく数を引いて降順にする。
(mDivNum + 1) - ( mActIdxZr % mDivNum );
}■alignCenter

XY配置を『ヌルを中心に中央ぞろえ』にする。
解説:これは上記までのインデックス変更ではなく、それを使って作った配置式を『ヌルの位置を変えれば移動できてかつ中央ぞろえ』にする方法です。
式のコメントの通り、最初に原点[0,0]基準の配置を作り、ヌル基準にしてヌルが左上に来る形にして、さらに配置全体の長さの半分をXYそれぞれに引くことで、中央ぞろえにしています。
mDivNum = 折り返す番号。
mMtplNum = 離したい距離。
//XにroopEach、YにroopMassを使用。距離を調整するためにmMtplNumを掛けます。
//この時点で、原点[0,0]基準の配置は完了しています。
X = ((mActIdx - 1) % mDivNum) * mMtplNum;
Y = ( Math.floor( (mActIdx - 1 ) / mDivNum ) ) * mMtplNum;
//XYそれぞれの、配置全体の長さの半分を出しておきます。
mLgtSumX = ( mMtplNum * ( mDivNum - 1 ) ) / 2;
mLgtSumY = (( Math.floor( (mActNumLyrs - 1 ) / mDivNum ) ) * mMtplNum) / 2;
//XYは原点基準の値なので、ヌル 1の位置を足してヌル 1基準にします。
//この時点でヌル 1が左上となる配置になります。
//さらに中央ぞろえにするために、配置全体の長さの半分を引いています。
mRstPt = mCtrlF.position + [X,Y] - [mLgtSumX,mLgtSumY];回転配置で使う関数
■mGetRotPt関数
function mGetRotPt ( aStdPt , aRot , aLgt ){
//aRotそのままだと、ゼロ度で横方向への位置となるので、上方向始まりとなるよう-90する。
var mDtoR = degreesToRadians( aRot - 90 );
var X = Math.cos( mDtoR ) * aLgt;
var Y = Math.sin( mDtoR ) * aLgt;
return ([X,Y] + aStdPt);
}使い方:この関数をエクスプレッションの一番上に置いて『変数 = mGetRotPt ( ヌルとかの基準位置 , 回転角度 , 基準位置からどれだけ離すかの距離 );』と書くと、変数に回転結果の位置が入ります。
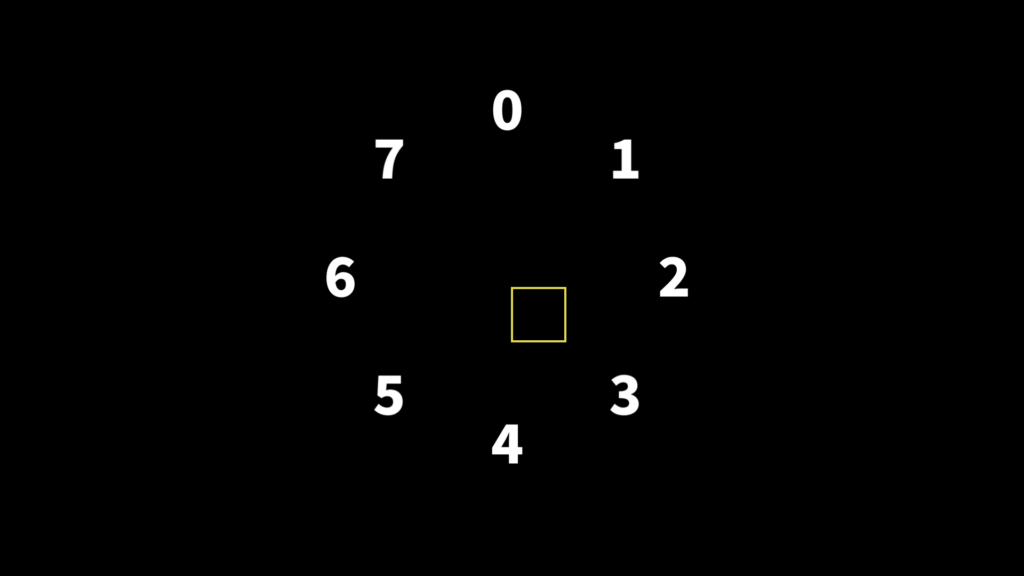
例:自動で円状配置したい場合、以下のような式で簡単に実現できます。レイヤー毎の角度は『360度をレイヤー総数で割った角度』となり、その角度×レイヤーインデックスでそのレイヤーが担当する角度がわかる、といった具合です。
function mGetRotPt ( aStdPt , aRot , aLgt ){
var mDtoR = degreesToRadians( aRot - 90 );
var X = Math.cos( mDtoR ) * aLgt;
var Y = Math.sin( mDtoR ) * aLgt;
return ([X,Y] + aStdPt);
}
mCtrlF = thisComp.layer("ヌル 1");
mCtrlL = thisComp.layer("ヌル 2");
mActIdx = index - mCtrlF.index;
mActNumLyrs = ( mCtrlL.index - mCtrlF.index ) -1;
//レイヤー毎の角度。
mRot = ( 360 / mActNumLyrs ) * ( mActIdx - 1 );
mLgt = 離したい距離;
//ヌル 1を円の中心とする。
mStdPt = mCtrlF.position;
mRstPt = mGetRotPt ( mStdPt , mRot , mLgt );以上です!
使いどころ
インデックス系エクスプレッションは上記のような式の組み合わせで色々なことができます。また、円状、XY配置問わず、自分で調整したい箇所はエクスプレッション制御に置き換えたり、加えたりして値を調整可能にできるので、便利ですね。
実はインデックスを使わなくても、整列させるエクスプレッションは作成可能です。例えば、1つ上のレイヤーの位置を取得して、それに、とある値をプラスしていく式を作れば可能ですね。しかし、これだと問題があります。『処理が重い』んですね…。1レイヤーを計算して値を出し、それを参照してまた値を出し…とやると重くなります。なので、レイヤーがもともと持っているインデックスを使ったほうが速いというわけですね。
整列以外にも、グラフ作りやディレイ処理など、色々とできるのでお試しください。